How To Choose Kernel Size For Laplacian Of Gaussian Filter
February 14, 2001
Lab 2
Laplacian filters are derivative filters used to find areas of rapid modify (edges) in images. Since derivative filters are very sensitive to noise, it is mutual to smooth the image (east.thou., using a Gaussian filter) earlier applying the Laplacian. This two-step process is phone call the Laplacian of Gaussian (LoG) performance.
In that location are different ways to detect an guess detached convolution kernal that approximates the event of the Laplacian. A possible kernel is
This is called a negative Laplacian because the fundamental superlative is negative. It is but as appropriate to contrary the signs of the elements, using -1s and a +4, to get a positive Laplacian. It doesn't matter.
To include a smoothing Gaussian filter, combine the Laplacian and Gaussian functions to obtain a single equation:
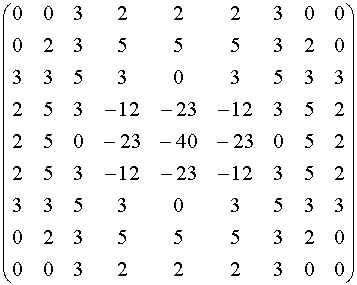
A detached kernel for the case of σ = one.4 is given by
The LoG operator takes the 2d derivative of the prototype. Where the image is basically uniform, the LoG will give zip. Wherever a modify occurs, the LoG will give a positive response on the darker side and a negative response on the lighter side. At a sharp edge between two regions, the response will be
When using the filter given above, or whatever other similar filter, the output can contain values that are quite large and may be negative, and so it is of import to utilise an paradigm type that supports negatives and a large range, and and then calibration the output. (ImageJ has a 32-fleck floating indicate representation). Alternatively, a scaling factor can be used on the filter to restrict the range of values.
Generate a LoG filter with Gaussian σ = 1.0, using a 7x7 kernel. Apply this filter to the image given beneath.
. 
What can y'all say about the output prototype? At present combine (subtract) the 2 images in an endeavour to sharpen the original epitome. You may have to calibration the filtered image before combining the ii images. Too, you lot may take to translate the filtered image by half the width of the convolution kernel in both the 10 and y directions in club to register the images correctly. A little experimentation may be required. Salvage the event you think is your best endeavor
The enhancement sharpens the edges but also increases noise. If the original prototype is filtered with a simple Laplacian (a LoG filter with a very narrow Gaussian), the resulting output is rather noisy. Combining this output with the original will requite a noisy result. On the other manus, using a larger σ for the Gaussian will reduce the dissonance, but the sharpening consequence volition be reduced. Life is full of compromises.
Concluding modified on March 21, 2001
How To Choose Kernel Size For Laplacian Of Gaussian Filter,
Source: https://academic.mu.edu/phys/matthysd/web226/Lab02.htm
Posted by: eadiebence1984.blogspot.com

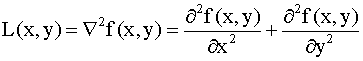
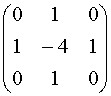
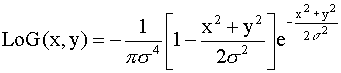

0 Response to "How To Choose Kernel Size For Laplacian Of Gaussian Filter"
Post a Comment